


I wrote a paper thats explains how an infinite number of points constitutes a finite space and that infinite spaces are mathematically undefined.
I made some changes in the results section and included a second version.
\(n/(x-1)\) is an extremely simple function that super-smart students don't bother to take its limit (it's not worth their effort). But it models a real physical phenomena and therefore gives results as far as to defining infinite space's nature.
You don't have to close the gaps with \(x-1\). You can fully close them with any way you want with any function with limits. I also used \(2^x\) to close the gaps. The trick here is to make gaps get equally smaller. All gaps have to have equal length while getting smaller equally.
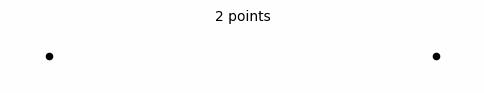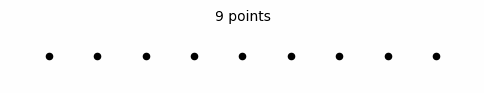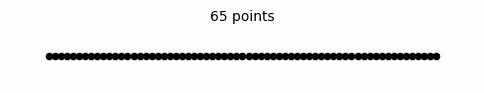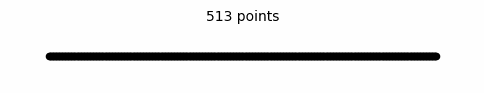
Since space is finite, coordinate system is finite. Here is the confusing part though, when x-axis is finite, limits should not reach infinity (there is no graph that extends infinitely where the limit can reach infinity), which makes building a continuous finite space not possible. But this is a paradox. You need to reach infinity to build a continuous finite space but that, in turn, means limits cannot approach infinity. However, it would theoretically be possible to build a space that is not continuous in case limits do not approach infinity.
Finite space construction isn't the only proof that outer space is finite. The other proof is much simpler and requires less rigorous analysis. You can multiply a finite line (a finite space) with any real number and the result is finite but not with infinity and that is the answer.
Former teachings of mathematical spaces taught us that space can be both finite and infinite. For example, they said the real number line extends infinitely in both directions while constituting an infinite space. I particularly want to falsify this statement. I earlier proved an infinite number of points make up a finite line. Therefore, if a line extends infinitely in one or both directions, that means that it cannot consist of points. But if a line consists of points— which we know is the case— then a line cannot extend infinitely in one or both directions. Since we know for sure that a line consists of points, then Euclidean space and thus outer space is finite.
Outer space has all properties of 3-D Euclidean space. I earlier proved that Euclidean space also has the finiteness property. Can we then say that outer space satisfies this property as well? If so, outer space as we perceive it is finite.
Even if you make the assumption that infinity as a concept exists (limits reaching infinity), spaces of all dimensions are still finite. If you accept that infinity doesn't exist, then spaces are finite anyway. We can conclude that mathematical infinity is not physically real; however, it remains a useful abstraction.
I would like to add one more thing: if a finite number of points constituted a continuous finite space, then we could say infinite space exists.
If we leave aside the effects of mass and energy described by Einstein's general theory of relativity, outer space satisfies all properties of Euclidean spaces. I have proved that Euclidean space's another property is that it must be finite. Could you then say for sure that outer space satisfies Euclidean space's finiteness property? If so, outer space as we perceive it is finite.
We know for sure that outer space satisfies all properties of Euclidean spaces except for finiteness property. Does the fact that outer space satisfies all properties of Euclidean spaces while leaving aside finiteness property mean that it would also have to satisfy finiteness property?
Note: Originally, my paper replaced n, which is the length of the line, with the infinity sign to indicate infinite length. However, generative AIs (Gemini, ChatGPT) say this isn't a correct operation because infinity is not a defined value that can be substituted into n -- which is the length of the space. I write my new equation here:
\[ \lim_{\substack{n\to \infty \\ x\to \infty}} \frac{n}{x-1} = \frac{\infty}{\infty} \]
I wrote a paper that explains why improper integrals do not exist.
Here is the paper.\[ \int_{\infty}^{\infty} f(x) \,dx = 1\]
If you have read the paper, you will know that the integral, as it is used in probability density functions (PDFs), is not technically meaningful by the definition of integral. Probability density function (PDF) can be as big as you want but not 1.
You would see that the integral will never take on the value 1 because integrals with infinite boundaries are undefined. If you want to use \(\infty\) notation, you should drop \(dx\), and should come up with a new concept.
\[\displaystyle {\widehat {f}}(\xi ) = \int _{-\infty }^{\infty }f(x)\ e^{-i2\pi \xi x} \,dx, \quad \forall \xi \in \mathbb {R} .\]
Fourier transform in its current from is not meaningful. Furthermore, you cannot numerically precisely compute an integral and take its limit to infinity. But fourier transform is useful and works within finite boundaries.
Interestingly, though, if rectangles (instead of \(dx\)) are used to approximate the integral, there will be an infinite number of rectangles between an infinite boundary - where there is no ambiguity as there is with \(dx\).
To eliminate error margin in derivative and integral, you need to reach infinity with limits. However, such use is not feasible in numerical computations. But you need to consider the fact that error margin could be as low as you wish it to be, and practical applications always tolerate error margin. Therefore, you can numerically compute derivative and integral in computers with adequate error margin. It is not possible to eliminate error margin in numerical computations because you cannot reach infinity, multiply (integral) or divide (derivative) by zero.
\[ \int_{a}^{b} f(x) \,dx = \lim_{n\to\infty} \sum_{i=1}^{n} f(x_i) * \frac{b-a}{n}\]
\[f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}\]
When you want to use the above formulas numerically in computers, you cannot divide by zero in the derivative definition or you cannot multiply by zero in the integral definition; however, you can place any value as small as you want in order to bring the error margin to the desired value. Considering practical applications always tolerate an error margin, you need not fully get rid of it. The important thing about symbolic mathematics is that you need to know the exact value of a derivative or an integral to be able to decide the error margin. But practical applications will always tolerate error margins that come as a result of numerical computations.
Therefore, we can say that numerical computations with error margins as low as we wish will always be adequate for practical applications. Symbolic math exists so that we can get precise values but nothing is precise in everyday applications.
Turkish is an agglutinative language and is heavily reliant on suffixes (although words formed with prefixes are used due to influence from other languages. You need to correctly hear and understand suffixes in order to understand Turkish. Modal verbs, tenses are all suffixes in Turkish. Auxiliary verbs as they are present in English are not present in Turkish. Turkish have no genders and adjectives do not change based on that (they do not agree with the noun). Turkish does have grammatical cases that are independent of genders and you need to know them correctly. However, the way they are taught in Turkish schools and language is completely different than how they are taught in Indo-European languages and European schools, therefore most Turks educated in Turkish schools fail to correctly understand Indo-European languages. Turkish has a strange way expressing the past that is not present in Indo-European languages that is simply called "heard past". Relative pronouns are not present in Turkish language as they are present in Indo-European languages. Turkish instead uses something called verbal adjectives with suffixes added to convey the same meaning. Turkish uses postpositions added as suffixes to the words instead of prepositions. Furthermore, the language uses subject-object-verb order but it is quite flexible like in Russian or German because of the case system present in the language. The only difference is that Turkish case system is independent of grammatical genders. Turkish creates challenges in understanding that are not present in Indo-European languages to due to heavy combinations of suffixes that totally alter the meaning. Even Turks themselves have trouble understanding their own materials at times. Turkish uses simple past for many actions including those that are expressed with present perfect. It has a second form of past that is not present in Indo-European languages and is hard to grasp for Indo-European speakers. You can't use infinitive clause to imply a purpose in Turkish. You need to explicitly use "for" in order to convey the same meaning. For example, you say "I came home for to eat". Saying "I came home to eat" will be unintelligible. Turkish language uses the same numbers as Kazakh, Turkmen, Uzbek, Kyrgyz, Azeri and other Turkic Siberian languages. If you know numbers in Turkish, you will understand numbers everywhere. Turkish numbers are quite systematic and easy. Azeri is quite intelligible to Turkish speakers, Turkmen and Uzbek are also fairly intelligible but you need to give some effort to be able to understand the Kazakh language. You can't understand Mongolian, Korean or Japanese if you already know Turkish. It is quite easy to read in Turkish because each letter represents a distinct sound (but there are a few exceptions). You combine pronunciation of each letter and you get a complete word. Suffixes aren't separated from the root word in the written language unless the word fullfills certain criterias such as being a name of a place or a person or an organization. Turkish grammar rules all revolve around suffixes and their accordance with the root word. You don't think in terms of genders in Turkish, everything is genderless. Postpositions in Turkish are relatively easier than prepositions in Indo-European languages and are quite straightforward and that's the main reason why Turkish speakers fail to correctly use prepositions in Indo-European languages. Turkish grammar is quite systematic and you can use it like a robot but people won't find it nice. Turkish does not have definite articles, therefore Turkish speakers always fail to correctly use definite articles in other languages. Understanding the root word is never enough in Turkish, you need to understand the word as a whole with all the distinct meanings of each suffix - but that creates challenges in understanding that are not present in Indo-European languages. And it becomes a real problem when you have many words like this in a sentence. The longer a sentence becomes, the more problematic it is. Translations between Indo-European languages are solid, however, translations between Indo-European languages and Turkish miss some really important context at times. Certain things are impossible to express. You need to express them the way Indo-European speakers will understand.
Turkish language has its weaknesses and strengths like all other languages. Some things are definitely more fun to express in Turkish if you understand Turkish at a native level. It is hard to speak Turkish or express yourselves if you have a regular American-British mentality. The real strength of Turkish lies in daily life, not in scientific or technical topics. Actually, Turkish is quite weak when it comes to scientific and technical topics although they tried very hard to catch up with the developed nations. In fact, Turkish made some really stupid attempts to turkify names that had Persian, Greek, Arabic, French, English or other origins. Turkish has tons of loanwords from other languages but Turkish republic at some point attempted to turkify their names. Turks speak and think with a different mentality than Western nations and it takes time to get used to it. Turkish is a rich language that allows people to express themselves in their daily lives. Turks are not particularly good at science, so Turkish, the language that belongs to Turkish society, fails to adequately express scientific and technical topics. But that does not mean it is a simple and primitive language, it is actually quite successful in helping people express themselves in their daily lives whether it be funny topics, needs, emotions, society problems, etc. Turks mostly fail to express their emotions that belong to Turkish society in other languages.
Extra knowledge: In German you modify the adjective or the article to indicate grammatical case. In Russian, you modify the noun and adjectives together. Turkish does not modify adjectives, there is no agreement between adjective and the noun it modifies, instead, you only need to modify noun with suffixes to indicate the case. Turkish has another past tense that is not present in Indo-European languages that you use to express a past you indirectly know about. They simply call it "heard past". Such use of past tense is hard for Indo-European speakers to grasp and correctly use. It is a must to be able to use cases correctly to make sense in the language. Apart from that, you need to correctly conjugate the main verb based on person, number, tense in order to sound correct and you can omit the subject. Most non-native speakers from Indo-European languages miserably fail at it and the mistake sounds quite sharp to native ears. Turkish is a highly inflected language like Russian and German and there are six cases in Turkish, namely : Nominative, Accusative, Locative, Ablative, Genitive, Instrumental. The verb is mostly at the end depending on your mood and things you want to stress. German and Russian speakers won't struggle a lot in the word order, the mentality in case use is similar.
Both in English and Turkish, you get to use the semantics that correspond to modal verbs and tenses with the main verb, they are not separated. However, in German, tenses and modal verbs are seperated from the main verb, thus creating an unnecessary confusion that isn't present in English, Russian and Turkish.
First and foremost, the thing you have to know about Russian is that it is a highly inflected language with 6 cases. Unlike inflected articles and adjectives in German, the noun and the adjective that agrees with the noun is inflected. Understanding inflections in Russian is the key to understanding Russian. Actually, if you are able to correctly understand all the inflections in the Russian language, there is not much to bother yourselves about. It has perfective and imperfective aspects of verbs, which are different from English. One thing that is nice about the Russian language is that it doesn't have a lot of compound verbs that separate themselves. Verbs are quite practical and easy to understand if you are able to perceive them correctly. It is a language in which you can understand everything word by word (if you understand inflections correctly though).
There is an abundance of resources on this one. There are already many resources. But I would stress that key to understanding German correctly is article knowledge because all cases are dependent on them. You neeed to know articles correctly to inflect adjectives and articles that indicate the case and build relative clause. If you are able to understand cases correctly (which requires article knowledge), you will have a lot less trouble understanding sentence constructs where the verb is either at the end, or the sentence is out of order, which is the main difficulty for English speakers trying to understand German language. You need to be able to correctly conjugate adjectives to indicate the correct case. Furthermore, infinitive clause is different from English. German uses "be able to" differently from English. In perfect tense, certain verbs use "to be" as auxiliary verb, and it becomes hard to get used to it. You need to know all 4 cases correctly. German modal verbs and their mentality work different from English. German doesn't have the distinction made in English made with "may" and "might", they approach this issue differently.
The Hizmet kids are excellent gamblers because getting a good place in OSYM's university entrance exam is a gambling. It is extremely hard to be in the first 1000 and be placed in a bachelor's degree that falls within that range. Gambling is forbidden in Turkiye (I don't like the name "Turkey" since it creates ambiguity in the meaning), but the Hizmet kids and the remaining Turkish kids who fall within first 1000 range are excellent gamblers. There is such an intense competition that you will never get in there unless you get lucky. If you are not a successful gambler, you will never be there. The thing is you can be the smartest student out there but you need to take risks in order to get something out of the exam. Considering China's and India's population, Chinese and Indian students are world-class gamblers. The best of them all end up in casinos in Las Vegas.
The experiment is about a dice being rolled many times and how it converges towards an expected value to show a fact. As many of you may have known, expected value in a casino is that you will always lose in the long term. It means the more you play, the more you lose without any chances of winning. I am trying to answer how you escape that and if there are any odds that you can win and profit. The very basic idea here is that you need to avoid expected average in order to profit, which means you need to gamble less. Experiments I include below show this fact. If you roll a dice continously, it will approach the expected value very fast as seen in the illustrations. However, when you place gaps in your games, meaning that you roll the dice less, you will deviate from expected value depending on how many times you played, meaning that you will hold some chance for profit.
Based on what I read in Google Gemini, Google Translate fails to correctly tokenize suffixes in Turkish, meaning that Google Translate fails to tokenize suffixes as Turks natively perceive them. An explanation about this is given by Google Gemini, but I don't know if Google Translate internals are the same and that if Google Gemini makes mistakes about its assertions.
My discrete math finding is to be included in discrete math course material and will be used in C library function malloc as well as in binary protocols in internet backbone. It will be used in C/C++, Java compilers, Python interpreter, processor pipelines, compression algorithms, and cryptology. It will also be used in the pharmaceutical, petroleum and chemical industries, in construction of gas pipelines, multi-speed transmission systems and nuclear reactors.
This was my university project that I made some research about (today generative AIs give really reasonable approaches on how to do it). You can share images with WhatsApp, Telegram, and Facebook with people ranging from a few hundred to hundreds of thousands. However, when you upload a JPEG image to their servers, the image gets compressed, and information you concealed in them via steganography becomes corrupt or lost. That's where compression-resistant steganography becomes important. The end-result of this project will be that when you upload a JPEG picture to Facebook, you will distribute concealed information to millions of people via your Facebook page. An algorithm that employs compression-resistant steganography could be used, or AIs could be trained to accomplish the same result with correct datasets. I lacked both the algorithm and machine learning fundamentals when I was interested in this project.
I demand mathematics awards for my findings in mathematics. Goddamn whites will give me math awards for both findings.
Ich bin US-Staatsbürger geworden.
Я стал гражданином США.
Despite all, I am unemployed and need employment and stable income.


